什么是線性回歸?
線性回歸(Linear regression)是一種利用線性函數對自變量(特征)和因變量之間的關系進行建模的方法。線性回歸是機器學習中一種廣泛使用的基本回歸算法。含有有多個特征的線性回歸稱為多元線性回歸。
假設有 nn 個特征(自變量)x1x1,x2x2,...,xnxn,一個輸出變量 yy,線性回歸的一般形式表示如下:
y=f(x)=w1x1+w2x2+...+wnxn+b .(1)(1)y=f(x)=w1x1+w2x2+...+wnxn+b .
其中,系數 w1w1,w2w2,...,wnwn 為特征的權重,bb 為偏置。
上式也可以寫成向量的形式:y=f(x)=wTx+b .(2)(2)y=f(x)=wTx+b .
其中,x=[x1,x2,...,xn]x=[x1,x2,...,xn],w=[w1,w2,...,wn]w=[w1,w2,...,wn].
看不懂吧,我也看不懂,直接上圖,有圖有真相。
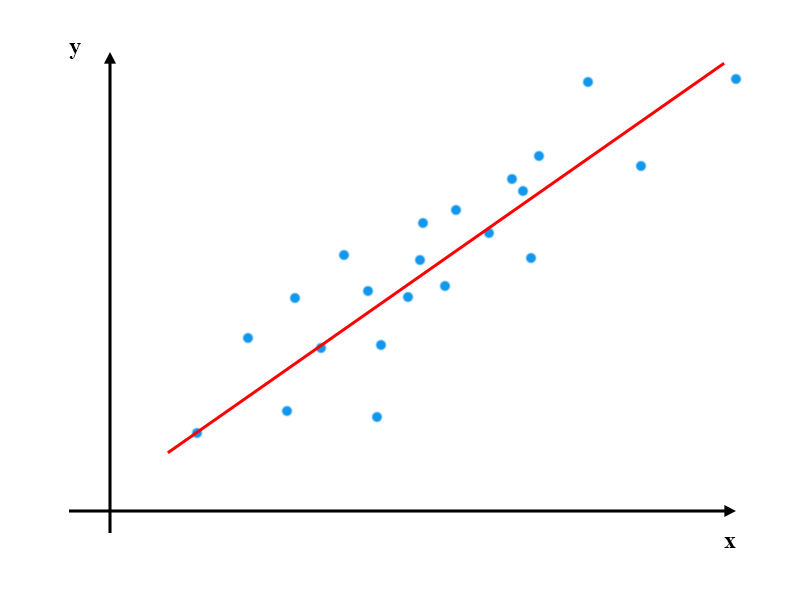
藍色表示數據點,紅色直線表示最終求得的線性回歸結果。
幾種線性回歸算法:
最小二乘法:
• 它通過 最小化誤差的平方和 ,尋找數據的最佳函數匹配。
• 利用最小二乘法可以簡便地求得未知的數據,并使得這些求得的數據與實際數據之間 誤差的平方 和 為最小。
• 假設我們現在有一系列的數據點(xi,yi) (i=1,…,m),那么由我們給出的擬合函數h(x)得到的估計量就是h(xi)
• 殘差:ri = h(xi) – yi
• 三種范數:
1. ∞-范數:殘差絕對值的最大值,即所有數據點中殘差距離的最大值:
2. 1-范數:絕對殘差和,即所有數據點殘差距離之和:
3. 2-范數:殘差平方和:
• 擬合程度,用通俗的話來講,就是我們的擬合函數h(x)與待求解的函數y之間的相似性。那么
2-范數越小,自然相似性就比較高了。
所以式子就可以寫為:
分別對k和b求偏導,然后令偏導數為0,即可獲得極值點。
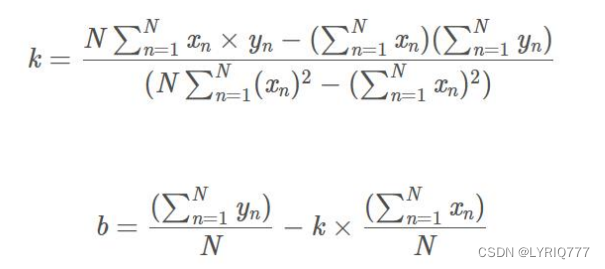
RANSAC:
• 隨機采樣一致性(random sample consensus)。
• RANSAC是一種思想 ,一個求解已知模型的參數的框架。 它不限定某一特定的問題,可以是計 算機視覺的問題,同樣也可以是統計數學,甚至可以是經濟學領域的模型參數估計問題。
• 它是一種迭代的方法,用來在一組包含離群的被觀測數據中估算出數學模型的參數。 RANSAC是一個非確定性算法,在某種意義上說,它會產生一個在一定概率下合理的結果,其允許使用更多次的迭代來使其概率增加。
• RANSAC的基本假設是 “內群”數據可以通過幾組模型參數來敘述其數據分布,而“離群”數據則是不適合模型化的數據。 數據會受噪聲影響,噪聲指的是離群,例如從極端的噪聲或錯誤解釋有關數據的測量或不正確的假設。 RANSAC假定,給定一組(通常很小的)內群,存在一個 程序,這個程序可以估算最佳解釋或最適用于這一數據模型的參數。
RANSAC算法的輸入:
1. 一組觀測數據(往往含有較大的噪聲或無效點),
2. 一個用于解釋觀測數據的參數化模型, 比如 y=ax+b
3. 一些可信的參數。
RANSAC 的步驟:
1. 在數據中隨機選擇幾個點設定為內群
2. 計算適合內群的模型 e.g. y=ax+b ->y=2x+3 y=4x+5
3. 把其它剛才沒選到的點帶入剛才建立的模型中,計算是否為內群 e.g. hi=2xi+3->ri
4. 記下內群數量
5. 重復以上步驟
6. 比較哪次計算中內群數量最多,內群最多的那次所建的模型就是我們所要求的解
注意 : 不同問題對應的數學模型不同,因此在計算模型參數時方法必定不同,RANSAC的作用不在于
計算模型參數。(這導致ransac的缺點在于要求數學模型已知)
這里有幾個問題:
1. 一開始的時候我們要隨機選擇多少點(n)
2. 以及要重復做多少次(k)
• 假設每個點是真正內群的概率為 w:
w = 內群的數目/(內群數目+外群數目)
• 通常我們不知道 w 是多少, w^n是所選擇的n個點都是內群的機率, 1-w^n 是所選擇的n個點至少有一個不是內群的機率, (1 − w^n)^k 是表示重復 k 次都沒有全部的n個點都是內群的機率, 假設算法跑 k 次以后成功的機率是p,那么,
1 − p = (1 − w^n)^k
p = 1 − (1 − w^n)^k
• 我們可以通過P反算得到抽取次數K,K=log(1-P)/log(1-w^n)。
• 所以如果希望成功機率高:
• 當n不變時,k越大,則p越大; 當w不變時,n越大,所需的k就越大。
• 通常w未知,所以n 選小一點比較好。
RANSAC 的優缺點:
優點:
1. 它能魯棒的估計模型參數。例如,它能從包含大量局外點的數據集中估計出高精度的參數。
缺點:
1. 它計算參數的迭代次數沒有上限;如果設置迭代次數的上限,得到的結果可能不是最優的結果,甚至可能得到錯誤的結果。
2. RANSAC只有一定的概率得到可信的模型,概率與迭代次數成正比。
3. 它要求設置跟問題相關的閥值。
4. RANSAC只能從特定的數據集中估計出一個模型,如果存在兩個(或多個)模型,RANSAC不能找到別的模型。
5. 要求數學模型已知
RANSAC 與最小二乘法
• 生產實踐中的數據往往會有一定的偏差。
• 例如我們知道兩個變量X與Y之間呈線性關系,Y=aX+b,我們想確定參數a與b的具體值。通過實驗,可以得到一組X與Y的測試值。雖然理論上兩個未知數的方程只需要兩組值即可確認,但由于系統誤差的原因,任意取兩點算出的a與b的值都不盡相同。我們希望的是,最后計算得出的理論模型與測試值的誤差最小。
• 最小二乘法:通過計算最小均方差關于參數a、b的偏導數為零時的值。事實上,很多情況下,最小二乘法都是線性回歸的代名詞。
• 遺憾的是,最小二乘法只適合于誤差較小的情況。
• 在模型確定以及最大迭代次數允許的情況下,RANSAC總是能找到最優解。(對于包含80%誤差的數據集,RANSAC的效果遠優于直接的最小二乘法。)
• 由于一張圖片中像素點數量大,采用最小二乘法運算量大,計算速度慢。
哈希算法:
1. 均值哈希算法aHash
步驟
1. 縮放:圖片縮放為8*8,保留結構,除去細節。
2. 灰度化:轉換為灰度圖。
3. 求平均值:計算灰度圖所有像素的平均值。
4. 比較:像素值大于平均值記作1,相反記作0,總共64位。
5. 生成hash:將上述步驟生成的1和0按順序組合起來既是圖片的指紋(hash)。
6. 對比指紋:將兩幅圖的指紋對比,計算漢明距離,即兩個64位的hash值有多少位是不一樣的,不相同位數越少,圖片越相似。
漢明距離
兩個整數之間的漢明距離指的是這兩個數字對應二進制位不同的位置的數目。
2. 差值哈希算法dHash
差值哈希算法相較于均值哈希算法,前期和后期基本相同,只有中間比較hash有變化。
步驟
1. 縮放:圖片縮放為 8*9 ,保留結構,除去細節。
2. 灰度化:轉換為灰度圖。
3. 求平均值:計算灰度圖所有像素的平均值。 ---這步沒有,只是為了與均值哈希做對比
4. 比較:像素值大于后一個像素值記作1,相反記作0。本行不與下一行對比,每行9個像素,
八個差值,有8行,總共64位
5. 生成hash:將上述步驟生成的1和0按順序組合起來既是圖片的指紋(hash)。
6. 對比指紋:將兩幅圖的指紋對比,計算漢明距離,即兩個64位的hash值有多少位是不一樣的,不相同位數越少,圖片越相似。
3. 感知哈希算法pHash
均值哈希算法過于嚴格,不夠精確,更適合搜索縮略圖,為了獲得更精確的結果可以選擇感知哈希
算法,它采用的是DCT(離散余弦變換)來降低頻率的方法。
步驟:
1. 縮小圖片:32 * 32是一個較好的大小,這樣方便DCT計算
2. 轉化為灰度圖:把縮放后的圖片轉化為灰度圖。
3. 計算DCT:DCT把圖片分離成分率的集合
4. 縮小DCT:DCT計算后的矩陣是32 * 32,保留左上角的8 * 8,這些代表圖片的最低頻率。
5. 計算平均值:計算縮小DCT后的所有像素點的平均值。
6. 進一步減小DCT:大于平均值記錄為1,反之記錄為0.
7. 得到信息指紋:組合64個信息位,順序隨意保持一致性。
8. 最后比對兩張圖片的指紋,獲得漢明距離即可。
離散余弦變換 DCT
| 
